Kointegrációs teszt az OECD által közölt termékenységi arányszámokon

Elméleti megfontolás

A termékenységi ráta és makrogazdasági mutatók közötti kapcsolat empirikus elemzése gyakorta történik az egyes országok adatain keresztmetszeti- vagy panelökonometria alkalmazásával. Mindazonáltal téves konklúziókra juthatunk az ilyen modellekből, mivel az egymáshoz közel lévő országok számos változó (pl.: kulturálisan, politikailag, gazdaságilag) mentén klasztereket képeznek, így torzulnak az előzetes modellfeltevéseink (Götmark & Andersson 2020:4). Annak érdekében, hogy ezt a hipotézist megerősítsem és ezzel az előbb említett országok adatain végzett elemzések mellett más modellezési stratégia mellett érveljek kointegrációs elemzést hajtok végre a termékenységi ráta idősorokon. Az eszközválasztás fő motivációja, hogy amennyiben két idősor között hosszútávon fennáll egy lineáris formában kifejezhető kapcsolat, úgy a kointegráció tesztelése során az ennek megfelelő nullhipotézis kerül elfogadásra (A bevett szakirodalommal szemben jelen tanulmányban KPSS-tesztel történik az Engel-Granger eljárás elvégzése). Ezen a ponton a kapcsolat fennállásában semmilyen közvetlen hatásmechanizmus feltevése nem indokolt, a nullhipotézis elfogadásának helyes értelmezése, hogy a két ország idősora nagyon hasonló pályát jár be (a benne lévő törések időben közel egybeesnek). Amennyiben Götmark és Andersson idézett feltevése helyes, úgy páronkénti tesztelés során az elemzés során gyakrabban kell egymással szomszédos országok között találnunk ilyen kapcsolatot találnunk.

A kointegráció módszertanának bemutatása

A kointegráció tesztelése három lépésből áll: (1) A két idősor azonos integráltságának ellenőrzése általánosított Dickey-Fuller teszt segítségével, majd (2) egy klasszikus legkisebb négyzetek (Ordinary Least Squares, OLS) modell becslése a két változó felhasználásával, egyiket eredményváltozónak választva, másikat magyarázóváltozónak egy konstans mellé. És végül (3) a modellből származó maradéktagok integráltságának megvizsgálása. Amennyiben a reziduumok éppen egyel alacsonyabb rendben integráltak, mint az összevetett idősorok, úgy a kointegráció fennáll a két változó között, a kettejük között húzódó hosszú távú kapcsolatot pedig az OLS koefficiensei írják le. Egy hipotetikus esetben például, ha a kointegráció léte megállapításra került, az OLS-ben pedig a regresszorhoz tartozó koefficiens értéke egy, miközben a konstanshoz tartozó érték szintén egy, akkor ez úgy értelmezhető, hogy a 2 idősor között fennáll hosszú távú kapcsolat, méghozzá úgy, hogy az OLS-ben függő változóként használt idősor értéke átlagosan eggyel nagyobb, mint azé, amelyiket magyarázóváltozóként vontunk be a modellbe. Az idősor ezen eszközének alkalmazása már feltételeket szab a vizsgált idősorokra: (1) A két összevetett változónak azonos rendben kell integráltnak lennie, azaz azonos számú differenciázás szükséges ahhoz, hogy az idősorokat stacionerré tegyük, és (2) ez a szám nem lehet nulla. Amennyiben a két kritérium valamelyike nem teljesül, úgy az itt leírt Engel-Granger eljárás egyáltalán nem elvégezhető. Jelen tanulmányban Kwiatkowski-Phillips-Schmidt-Shin (KPSS) tesztet alkalmazok az idősorok integráltságának meghatározására, miután a módszertan szakirodalma alapján kointegrációs kapcsolat megállítására ez a legjobban teljesítő teszt (Clegg 2014). Ez alapján a második kritérium nem jelent gondot, mivel az OECD oldalán elérhető 52 ország termékenységi rátájának egyike sem stacioner, továbbá 33 közülük elsőrendben, a maradék pedig másodrendben integrált.

Általános modell bemutatása

A kointegráció tesztelésének egy példáját mutatom be Magyarország és Lengyelország termékenységi rátája között. Az általános bemutatáshoz azért esett ezen két idősorra választásom, mert a későbbiekben kifejtésre kerülő eredményekből a kointegráció ténye itt megállapításra került. A kointegráció tesztelésének mindhárom lépését prezentálja a 2. ábra.

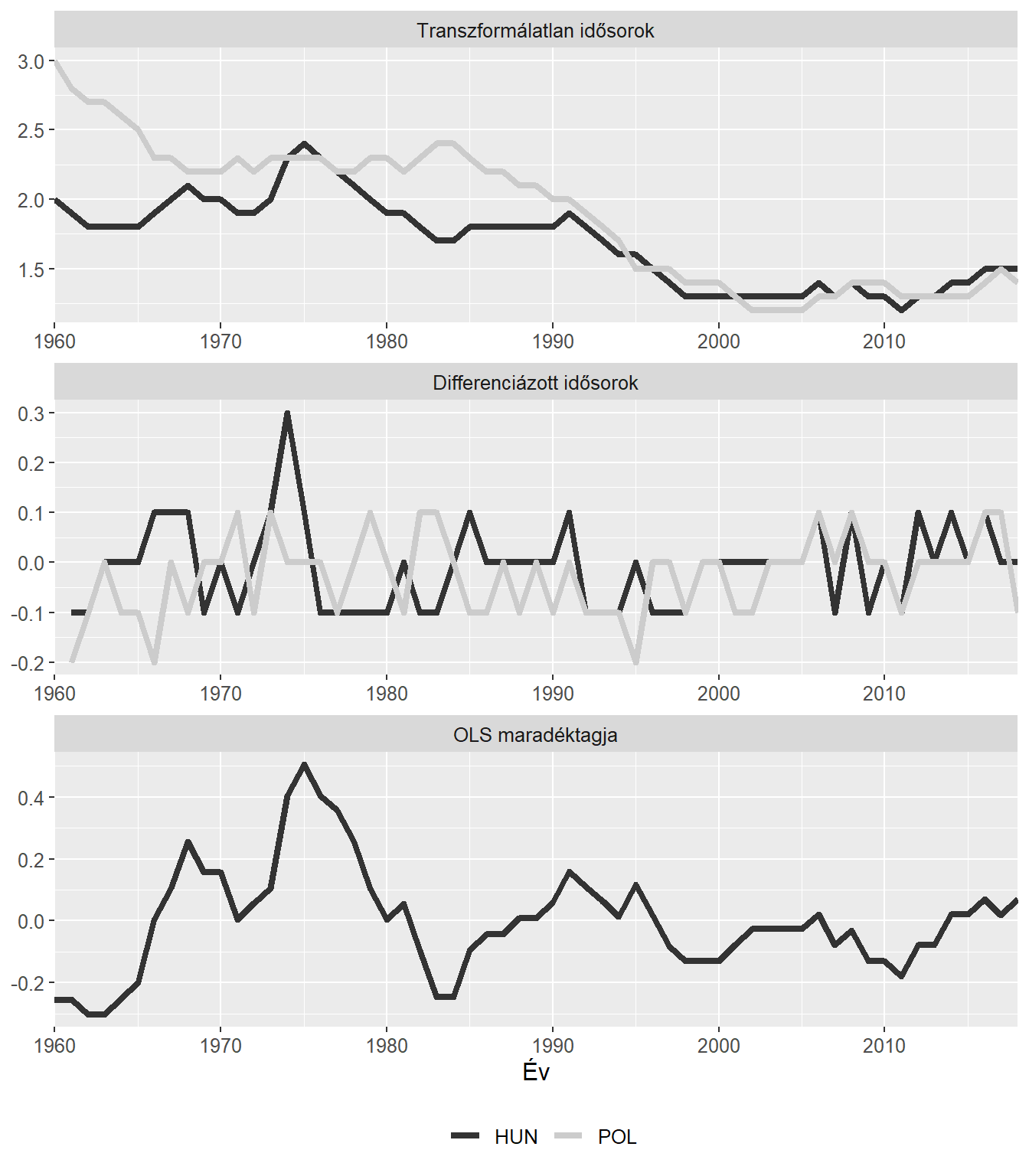
A magyar és lengyel TTA idősorok között fennálló kointegráció

Ábra 2: A magyar és lengyel TTA idősorok között fennálló kointegráció

A 2. ábra első paneljében láthatóak az eredeti idősoraink. Jól látható módon valóban hasonló pályát futottak, és mindkettőjük integráltságának foka biztosan nagyobb, mint egy. A KPSS-tesztek elvégzése során a magyar és a cseh TTA-ról is bebizonyosodott, hogy integráltságuk foka egy, így a teszt következő lépése következhet (a differenciázott idősorok stacioner tulajdonságát a 2. ábra második panelje mutatja be). Ebben az esetben Lengyelország termékenységi rátájának idősorát alkalmaztam regresszorként és a magyar idősor szerepelt a modellben eredményváltozóként. A megbecsült OLS modell hibatagját a 2. ábra harmadik panelje tartalmazza. A modell reziduumainak stacioner tulajdonsága pedig az elvégzett KPSS-teszt alapján bebizonyosodott, tehát a két idősor között a vizsgált időszakban fennállt egy tartós hosszú távú kapcsolat.

Modellbecslés és hipotézisvizsgálat

Az imént bemutatott általános modell lefuttatásra került az OECD honlapján elérhető 52 ország termékenységi rátájának idősorából készíthető összes párosításon. A tesztek végrehajtása során minden alkalommal KPSS-teszt került végrehajtásra és 5%-os szignifikanciaszinten lettek a döntések meghozva. A kointegrációs tesztek eredményét az 3. ábra szemlélteti.

df <- NeighbourCountry %>%
  mutate(x = names(NeighbourCountry)) %>%
  pivot_longer(-x, names_to = "y", values_to = "neighbour") %>%
  mutate(
    neighbour = ifelse(is.na(neighbour), "Nem határosak", "Határosak"),
    neighbour = ifelse(x == y, NA, neighbour)
  ) %>%
  merge(
    oecd_fertility %>% group_by(location) %>%
      summarise(d = ndiffs(tfr, test = "kpss", type = "level", alpha = .05)) %>%
      set_names("y", "dy")
  ) %>%
  merge(
    oecd_fertility %>% group_by(location) %>%
      summarise(d = ndiffs(tfr, test = "kpss", type = "level", alpha = .05)) %>%
      set_names("x", "dx")
  )

v <- vector() # collector vector
for (i in 1:nrow(df)) {
  if (df$dx[i] == df$dy[i] & df$x[i] != df$y[i]) {
    res <- oecd_fertility %>%
      pivot_wider(names_from = "location", values_from = "tfr") %>%
      dplyr::select(df$x[i], df$y[i]) %>%
      set_names(c("x", "y")) %>%
      na.exclude() %>%
      lm(formula = y ~ x) %>%
      .$residuals
    
    if (ndiffs(res, test = "kpss", type = "level", alpha = .05) < df$dx[i]) {
      v[i] <- "Kointegráltak"
    } else {
      v[i] <- "Nem kointegráltak"
    }
  } else {
    v[i] <- "A teszt nem elvégezhető"
  }
}

df$coint <- v

df <- merge(df, oecd_fertility %>%
              pivot_wider(names_from = "location", values_from = "tfr") %>%
              dplyr::select(-1) %>% cor(use = "pairwise.complete.obs") %>%
              data.frame() %>% rownames_to_column(var = "x") %>%
              pivot_longer(-1, names_to = "y", values_to = "cor"))

ggplot(data = df) +
  geom_tile(aes(x = x, y = y, fill = coint), color = "black") +
  labs(x = "", y = "", fill = "") +
  scale_fill_manual(values = c("white", "black", "grey")) +
  theme(axis.text.x = element_text(angle = 90, vjust = 0.45))
Kointegrációs tesztek eredményei

Ábra 3: Kointegrációs tesztek eredményei

Eredmények értelmezése, következtetések levonása

Az elemzés végrehajtása előtt megfogalmazott hipotézis ellenőrzéséhez szükséges meghatározni, hogy mely országok szomszédosok egymással. Ez szárazföldi határok esetén egyszerű, víziek esetében azonban szubjektívvé válik, ami torzítás forrása lehet. A szomszédossági kapcsolatokat magam rajzolom meg, a 4. ábra vizuális segédlet ehhez. A reprodukálhatóság érdekében a lista elérhető a csatolt GitHub repoban.

Számítások során egymás szomszédjának tekintett országok hálója

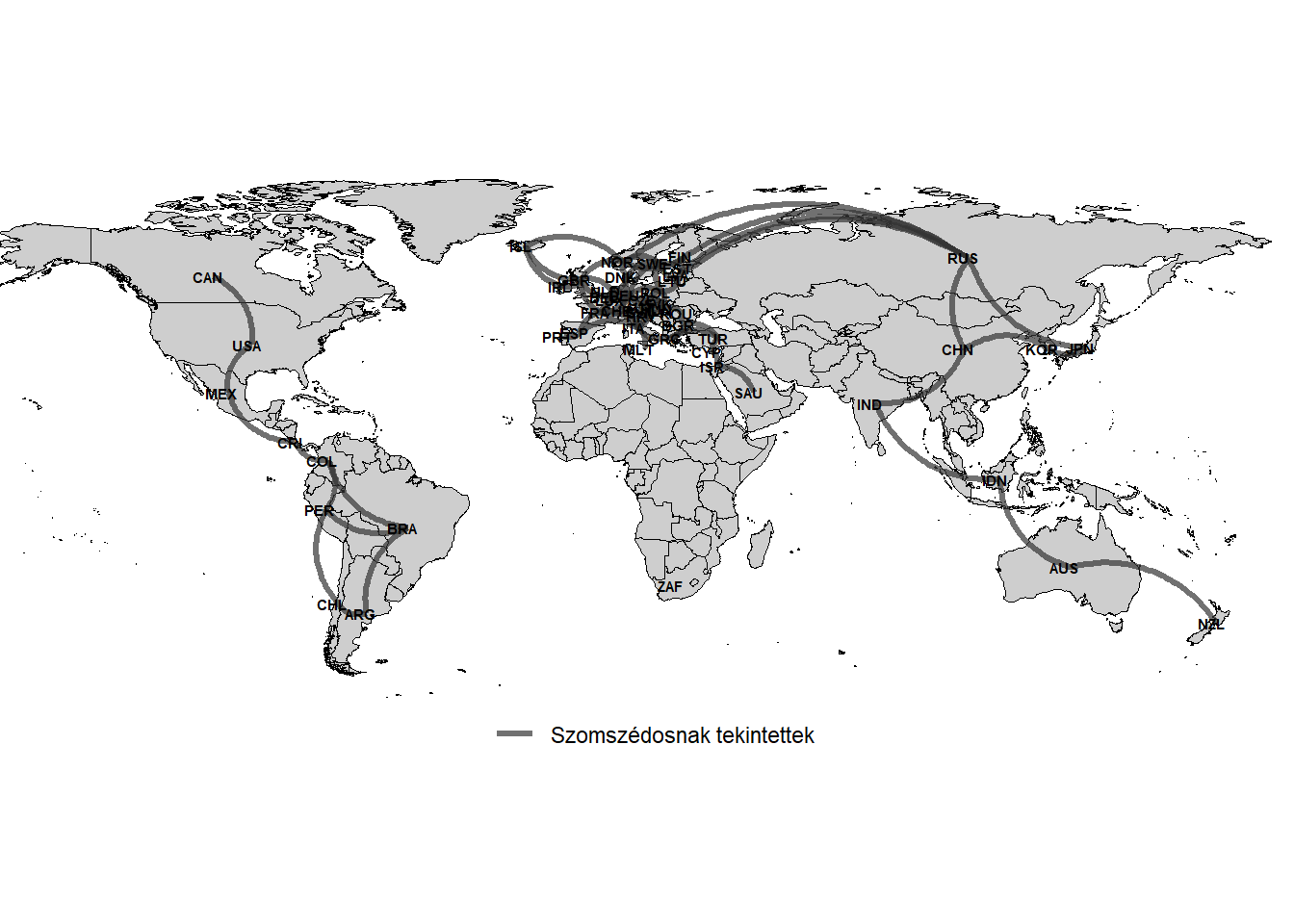
Ábra 4: Számítások során egymás szomszédjának tekintett országok hálója

Mind a lehetséges 2652 párosítás eredményét megvizsgálva és rendezve aszerint, hogy szomszédosok voltak-e az országok vagy sem azt kapjuk, hogy valóban szignifikánsan nagyobb a kointegráló idősor párok aránya ott, ahol a határok érintkeznek. Ezt a végső eredményt mutatja be a 1. táblázat. Az, hogy a nem elvégezhető tesztek aránya is magasabb ott, ahol az ország párok nem határosak egymással is ugyanezt a következtetést erősíti meg, mivel ez az jelenti, hogy egymással szomszédos országok gyakrabban azonos rendben integráltak, tehát jobban hasonlít egymásra az elmúlt 60 évben bejárt pályájuk. Szintén ebbe az irányba mutat, hogy az országok közötti lineáris korrelációs együtthatók átlaga is 10 %p-al magasabb a szomszéd párok körében (0,826 és 0,722).

Táblázat 1: Tesztek eredményeinek arányai egymással határos és nem határos országok esetében
Határosak Nem határosak
A teszt nem elvégezhető 32,2% 49,4%
Nem kointegráltak 27,6% 27,9%
Kointegráltak 40,2% 22,7%

Az elvégzett modellezésből egy másik kinyert eredmény, hogy a Magyarország termékenységi rátája kointegrál több környező szintén posztszocialista országéval, mint Szlovákia, Horvátország, Lengyelország. A 2. ábrán látszik, hogy ennek fontos pontja a 90-es években való csökkenés a termékenységi rátában. Ennek magyarázata a foglalkoztatás és szociális juttatások csökkentése, az egy főre jutó reáljövedelem csökkenése és a rendszerváltással felerősödő nyugati kultúra (pl.: a gyermektelenség) felé való húzás (Tárkányi 2008:432-435).