Magyarországi idősoros adatok elemzése vektor autoregresszív modellel

Elméleti megfontolás

A következőkben a magyar termékenységi ráta, az egy főre eső GDP és a munkanélküliségi ráta közötti kapcsolatot kívánom elemezni vektor autoregresszív modellel. Választásom azért esett erre az eszközre, mert (1) Granger-okság tesztelésével minden irányba ellenőrizhetőek a hatások, (2) varianciadekompozícióval az egyes változók relatív fontossága is meghatározható, továbbá impulzus válaszfüggvények segítségével nemcsak egy adott évre adható előrejelzés egy sokk következtében, de annak lecsengési üteme is kirajzolódik.

A vektor autoregresszív modell módszertanának bemutatása

Az ebben a fejezetben alkalmazott modellek első lépése, hogy készíteni kell egy vektor autoregresszív modellt (VAR), amelyen oksági tesztet végzünk. A VAR-modellekben több idősor együttesen szerepel, és alapesetben valamennyien endogén változói a modellnek, tehát a mutatók egyes időpontokhoz tartozó értékei a modellben kerülnek meghatározásra és nem külsőleg kerülnek be. A modell elkészítéséhez a benne foglalt változók körén túl egy késleltetési paraméter (p) meghatározása szükséges, amely bevett módon valamely információs kritériumon alapszik. Ebben a tanulmányban én az Akaike-féle információs kritériumot alkalmazom. A modell tartalmilag egy olyan rendszer felépítését jelenti, ahol minden változó legutolsó p darab értékeinek sorozata hatással van saját magára és minden más változó tárgyévének meghatározására. Tehát a modellben minden változó t-edik évi értéke2 úgy határozódik meg, hogy az összes változó p évet visszamenő értékének hatásainak eredőjét vesszük. Fontos azt megjegyezni, hogy egy változó értékére t-edik évben nem lehet hatással más változók t-edik évi értéke . A modell becslésnek azonban feltétele, hogy a bevont változók mind stacionerek legyenek, így előtte megfelelő számú differenciálással el kell érni. Az így felállított modelleken hajtottam végre a Granger-oksági teszteket. A teszt nem más, mint egy F-próba melynek nullhipotézise, hogy a vizsgált okozati változóra a modell becslése alapján felírt egyenletben oksági tényezőként tesztelt változó minden késleltetett értékéhez tartozó paraméter értéke nem különbözik statisztikailag szignifikánsan a nullától. Granger értelemben vett okság akkor áll fenn, ha ez a nullhipotézis elutasításra kerül, melynek interpretálása, hogy az eredményváltozóként tesztelt mutató jövőbeli értékére vonatkozóan csökken a bizonytalanság a magyarázó változó jelen, illetve múltbeli értékeinek ismeretében. Az elemzés eredményeinek megfelelően a helyen kezeléséhez szükséges hangsúlyozni, hogy a Granger-okság fennállása nem abban értelemben jelent kauzalitást, hogy a magyarázó változó valóban a kiváltó ok lenne a függő változó elváltozásában, csupán azt, hogy időben változása megelőzi azt, így előrejelzésében hasznosnak bizonyul. Ezzel azonban már meghaladja a korreláció interpretálhatóságát, miután az ok-okozati viszonyban betöltött szerepek identifikálhatóvá válnak. Az így elvégzett F-próbák csak késleltetett hatások eredményének megítélésére alkalmasak. Az egyidejű Granger-okság fennállásának tesztelése azon alapul, hogy a modellben endogén módon meghatározódó idősorok valós értéküktől vett eltéréseik mutatnak-e együttmozgást. Ebből következik, hogy míg az általános Granger-okság feltárja a kauzalitás irányát, addig az egyidejű Granger-okság szimmetrikus. Mindazonáltal fennállása esetén elméleti megfontolásból az okozat szerepét nem nyilvánítanám a TTA-ra, mivel a fogantatásnak időben biztosan korábban kellett megtörténnie. A VAR-modellekkel kapcsolatosan általánosan az a gyakorlati probléma, hogy rengeteg paramétert tartalmaznak. Az együtthatók számára vonatkozóan korlátozásokat nem tartalmazó modellek előrejelzés tekintetében is rosszul teljesítenek, de a bennük keletkező magas mértékű multikollinearitás az értelmezést is bonyolítja, míg alacsony késleltetés mellett a paraméterek becslése torzítottá válik (Maddala 2004). Így a vektor-autoregresszív modellek paramétereinek vizsgálata helyett az impulzus válaszfüggvényeket érdemes vizsgálat alá vetni. Az impulzus válaszfüggvény (IRF) azt mutatja be, hogy egy tárgyalt változónak a modellből származó reziduumainak szórásának egyenértékű sokk hatására miként reagál az egész rendszer, így a hatások iránya és lecsengése is megjelenítésre kerül. A modellből továbbá meghatározható az előrejelzés varianciadekompozíciója, amely megadja, hogy egy adott változó adott év múlvai érték varianciáját hány százalékban magyarázza, ily módon a változók között egy előrejelzés tekintetében relatív fontosság is felállítható.

Modellbecslés, hipotézisvizsgálat, eredmények értelmezése

Felhasználva mind a munkanélküliségi rátát, mind az egy főre eső bruttó kibocsátást, azzal a problémával szembesülünk, hogy előbbi idősor hossza igen rövid, mindössze 1999-ben kezdődik. Így adódik annak szükségessé, hogy az egy főre jutó GDP-vel, kihagyva a munkanélküliségi rátát is modell készüljön, hiszen annak láncindexe elérhető 1960-ig visszamenőleg is.

Csak egy főre jutó GDP-t és TTA-t tartalmazó modell

irf_plot <- function(model, n.ahead = 10, ci = .95,
                     plot_filter = NULL, n.col = NULL) {
  irf <- model %>%
    vars::irf(n.ahead = n.ahead, ci = ci)
  
  point <- irf %>%
    .$irf %>%
    do.call(what = rbind) %>%
    data.frame()
  
  point <- point %>%
    mutate(
      shock = rep(names(point), each = nrow(point) / length(point)),
      t = rep(0:(nrow(point) / length(point) - 1), times = length(point))
    ) %>%
    pivot_longer(cols = seq_along(point)) %>%
    transmute(
      t = t,
      variable = str_c(shock, " › ", name),
      point = value
    )
  
  lower <- irf %>%
    .$Lower %>%
    do.call(what = rbind) %>%
    data.frame()
  
  lower <- lower %>%
    mutate(
      shock = rep(names(lower), each = nrow(lower) / length(lower)),
      t = rep(0:(nrow(lower) / length(lower) - 1), times = length(lower))
    ) %>%
    pivot_longer(cols = seq_along(lower)) %>%
    transmute(
      t = t,
      variable = str_c(shock, " › ", name),
      lower = value
    )
  
  upper <- irf %>%
    .$Upper %>%
    do.call(what = rbind) %>%
    data.frame()
  
  upper <- upper %>%
    mutate(
      shock = rep(names(upper), each = nrow(upper) / length(upper)),
      t = rep(0:(nrow(upper) / length(upper) - 1), times = length(upper))
    ) %>%
    pivot_longer(cols = seq_along(upper)) %>%
    transmute(
      t = t,
      variable = str_c(shock, " › ", name),
      upper = value
    )
  
  df <- merge(point, lower, by = c("t", "variable")) %>%
    merge(upper, by = c("t", "variable")) %>%
    arrange(variable)
  
  if (!is.null(plot_filter)) {
    df <- df %>% filter(variable %in% unique(variable)[plot_filter])
  }
  
  if (is.null(n.col)) {
    n.col <- (n_distinct(df$variable)^0.5 %/% 1)
  }
  
  df %>% ggplot() +
    geom_hline(yintercept = 0, linetype = "dotted", size = 1) +
    geom_ribbon(aes(min = lower, max = upper, x = t,
     fill = paste(scales::percent(ci), "konfidencia intervallum")), alpha = .2) +
    geom_line(aes(x = t, y = point, color = "irf"), size = 1.2) +
    facet_wrap(vars(variable), scales = "free", ncol = n.col) +
    scale_color_manual(values = c("irf" = "black")) +
    scale_fill_manual(values = "grey50") +
    scale_x_continuous(breaks = 0:n.ahead, labels = 0:n.ahead,
                       expand = c(0, 0)) +
    labs(x = "", y = "", fill = NULL, color = NULL)
}

A modell feltétel biztosítása érdekében a Kwiatkowski-Phillips-Schmidt-Shin tesztek alapján mind a GDP/fő láncindexének, mind a TTA-nak differenciázása szükséges. Minden információs kritérium (AIC, HQ, SC, FPE) alapján egy a megfelelő késleltetés szám. Az modell gyökei jóval egy alattiak, így minden modellezési kritérium teljesül. A modell eredményei az előzetesen vártnak megfelelőek: (1) a TTA nem oka Granger értelemben az egy főre eső GDP-nek, míg (2) a GDP/fő a termékenységi rátának igen, (3) egyidejű okság nem áll fenn. (4) A GDP/fő differenciázott idősorának emelkedése a termékenységi ráta trendjét emeli, ezt a kapcsolatot mutatja be a 5. ábra.

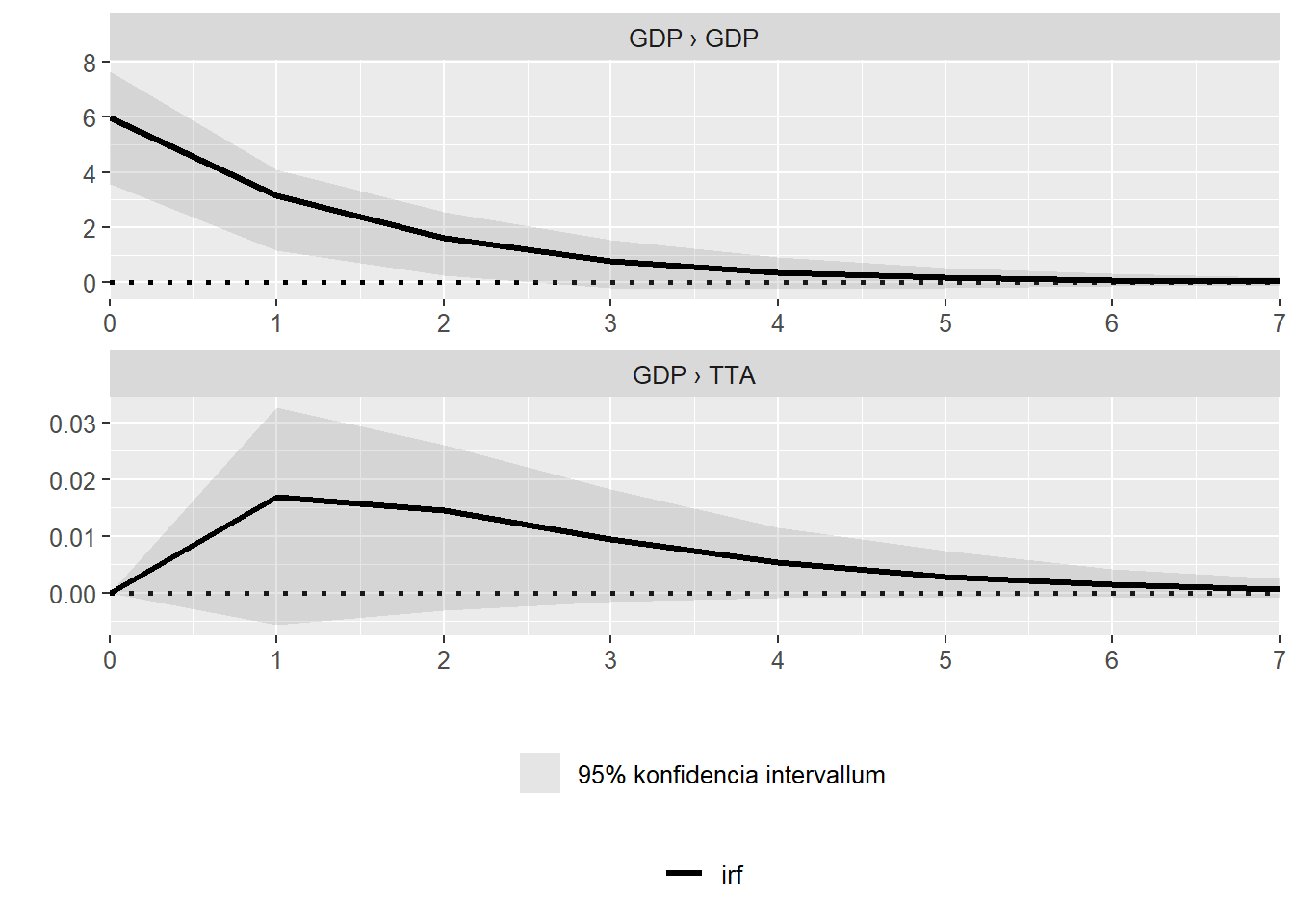
GDP/fő és TTA-t tartalmazó VAR modellből számított impulzus válaszfüggvények

Ábra 5: GDP/fő és TTA-t tartalmazó VAR modellből számított impulzus válaszfüggvények

A varianciadekompozíció alapján (5) a GDP/fő idősora 5%-ban magyarázza az egy évvel későbbi, 8,5%-ban a két évvel későbbi és 10%-ban a még későbbi értékeit a TTA magyarázott varianciájának. A fennmaradó rész a TTA jelen, illetve egy évvel korábbi értékeihez tartozik.

Az egy főre jutó GDP-t, munkanélküliségi rátát és TTA-t tartalmazó modell

Az egységgyök tesztek alapján az újonnan bejövő változót, a munkanélküliségi rátát nem szükséges differenciázni, mivel az stacioner. Ahogyan arra fentebb már említés került, a VAR modellek fő problémája, hogy rengeteg paramétert tartalmaznak. Már három változó esetén is annyit, hogy egynél nagyobb késleltetésre a munkanélküliségi ráta idősorának rövidsége miatt nincs lehetőség, így ez modell kerül kiválasztásra. Ez nagy hátránya a modellnek, de érdemes figyelembe venni, hogy az előző modellben, ahol még bőven megbecsülhető a VAR modell nagyobb késleltetés mellett is, szintén egy lett a maximális késleltetés szám az információs kritériumok alapján. A modell gyökei továbbra is jóval egy alatt maradnak.

Az modell eredményei a következők: (1) mind a munkanélküliségi ráta, mind a GDP/fő Granger értelemben oka a TTA-nak, és (2) ezen kívül nincs más oksági kapcsolat a modellben. A GDP/fő differenciázott idősorának emelkedése a termékenységi ráta trendjét ebben a modellben is emeli, egy munkanélküliséget megemelő sokk pedig csökkenti a TTA trendjének értékét. A varianciadekompozíció alapján a GDP/fő értéke lényegesen meghatározóbb, mint a munkanélküliségi rátáé. Az egyes sokkok lecsapódását a 6. ábra mutatja be.

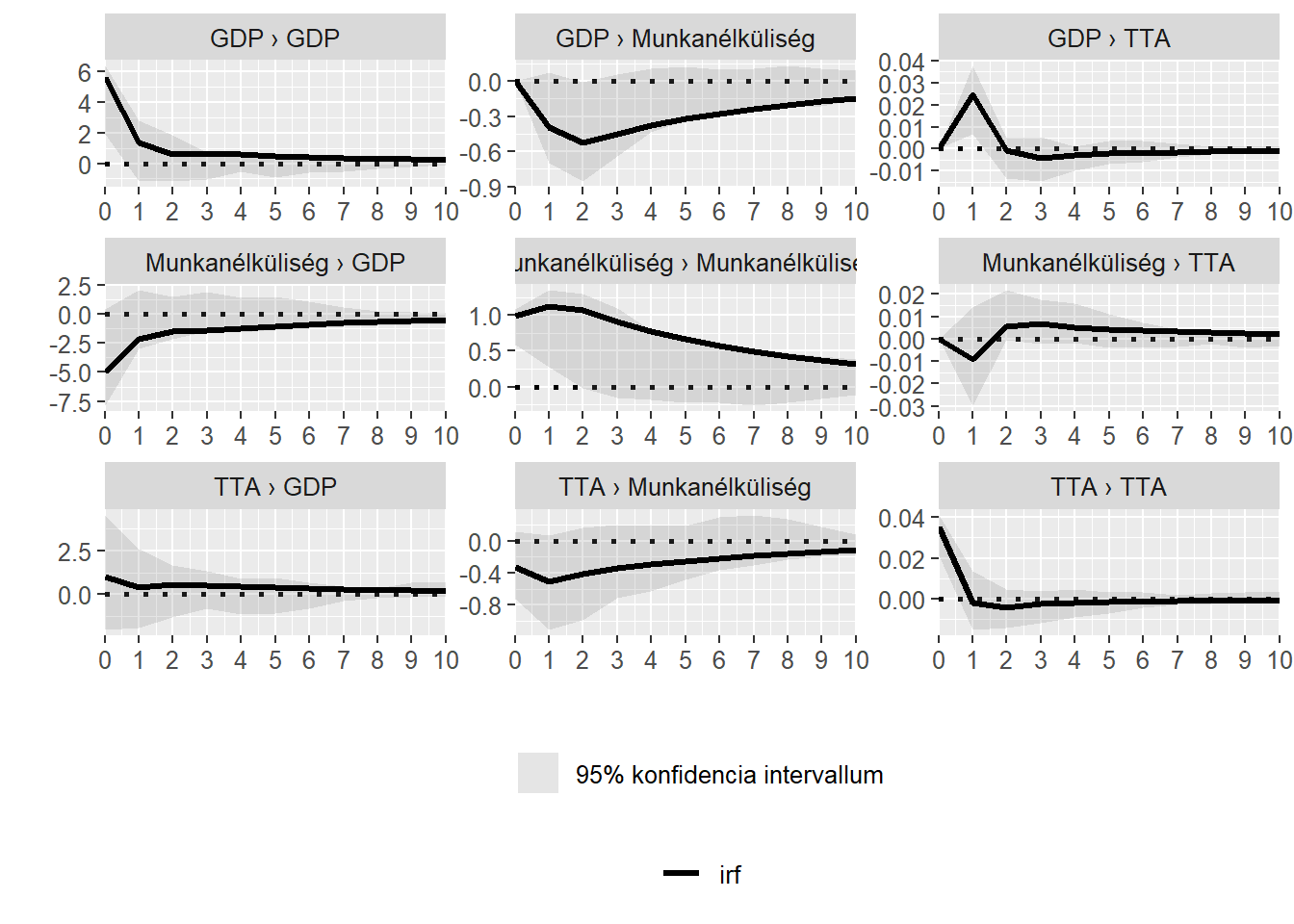
GDP/fő, munkanélküliségi rátát és TTA-t tartalmazó VAR modellből számított impulzus válaszfüggvények

Ábra 6: GDP/fő, munkanélküliségi rátát és TTA-t tartalmazó VAR modellből számított impulzus válaszfüggvények

A varianciadekompozíció alapján a GDP/fő értéke lényegesen meghatározóbb, mint a munkanélküliségi rátáé. A magyarázott variancia alakulását a 7. ábra ismerteti. Jól kivehető rajta, hogy az előző esethez képest a GDP/fő magyarázóereje szignifikánsan nőtt. Az egy évvel későbbi értéknek 31,41%-át magyarázza.

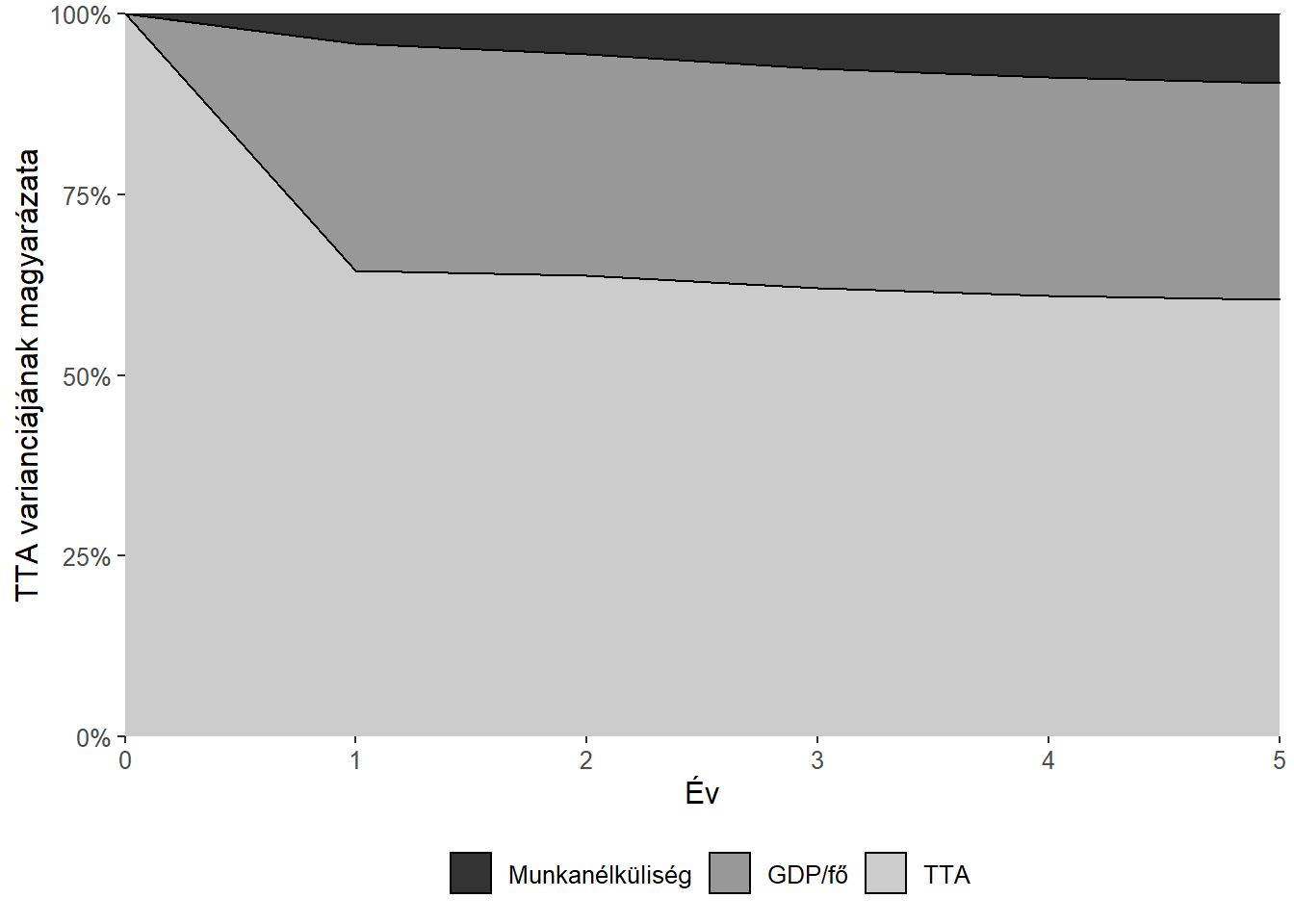
GDP/fő, munkanélküliségi rátát és TTA-t tartalmazó VAR modellből számított varianciadekompozíció

Ábra 7: GDP/fő, munkanélküliségi rátát és TTA-t tartalmazó VAR modellből számított varianciadekompozíció

  1. Ennek a szimultaneitás problémájának modellezési vonzata az oka, termesztésen elképzelhető olyan eset, hogy a születésszám hirtelen megugrása egy gazdasági vagy társadalmi mutatót már a tárgyalt évben befolyásol. Ennek vizsgálati módszerét a későbbiekben fejtem ki.↩