Magyarországi panel adatok
Elméleti megfontolás
A tanulmány ezen részében a teljes termékenységi arányszám, az egy főre GDP és a munkanélküliség magyarországi megyei szintű adatain folytatom az elemzést. TTA és GDP/fő adatok 2005-től 2018-ig, munkanélküliségi ráta 2006-tól 2019-ig volt elérhető számomra megyei bontásban, így panelökonometriai eszközök alkalmazására nyílik lehetőség. A fő motiváció ezen elemzés mögött, hogy a fentebb idősoros eszközökkel kinyert következtetések nagyobb mintaelemszámmal is megerősítést (vagy cáfolást) nyerjenek, illetve további ismeretek nyerhetők ki a hatások terület koncentrációja mentén.
Módszertan bemutatása
A lehetséges panelmodellek közül az alábbiakat vetem össze: ömlesztett modell, fixhatás-modell, véletlenhatás-modell. Az ömlesztett modell esetében minden megfigyelés ugyanazon konstanssal és magyarázóváltozókhoz tartozó paraméterekkel kerül meghatározásra. A fixhatás-modellnél az egyes megyékhez tartozó konstansok már eltérőek, mindegyik egyéni tengelymetszettel rendelkezik, de a magyarázóváltozókhoz tartozó paraméterek mindnél ugyanazok (a hatások fixálva vannak). A véletlenhatás-modell az előbbitől abban különbözik, hogy az egyéni konstansokat egy normális eloszlású véletlen folyamat által generált realizációknak tekintjük, így a becslés matematikája változik. A három modell közötti választás statisztikai tesztek alapján történik. Elsőként a Chow-tesztet végzem el, melynek nullhipotézise, hogy az ömlesztett modellt érdemes alkalmazni, majd elutasítás esetén a Hausman-tesztet, melynek nullhipotézise, hogy a véletlenhatás-modell felhasználása szükséges. Mindkét teszt nullhipotézisének elutasítása esetén a fixhatás-modell becslésére kerül sor. A magyarázóváltozók halmazának kiválasztását bonyolítja, hogy a fentebb bemutatott VAR modellek eredményei alapján a GDP/fő és a munkanélküliség késletetett változóit érdemes felhasználni. Ezzel ugyanis már nem választható ki modell egy információs kritérium minimalizálási céllal, mert a legnagyobb késleltetésű magyarázóváltozó megváltozásával az eredményváltozó is megváltozik, így az összehasonlítás nem lenne megfelelő. A változószelekció során ezért a paraméterek szignifikanciájára és a korrigált \(R^2\)-re fordítok figyelmet.
Modellbecslés és hipotézisvizsgálat
Mivel információs kritérium alapú modellszelekció a késleltetett magyarázó változók miatt nem kivitelezhető, így a fentebb leírtaknak megfelelően több modell is megbecslésre kerül. Mindegyik modell esetében a felhasznált magyarázóváltozók körének meghatározása után elvégzem a Chow- és Hausman-tesztet. A becsült négy modell esetében kivétel nélkül elutasításra kerül mindkét teszt nullhipotézise, így a fixhatású-modell alkalmazása indokolt. A 2. táblázat ismerteti az egyes fixhatású-modellek becsült paramétereit, illetve modell jellemzőket, köztük a két modellválasztási teszt p-értékét és a fixhatású-modell korrigált \(R^2\) értékét.
c.panel.extended <- c.panel %>%
transmute(
county, year, tfr, GDPcap,
GDPcap2 = GDPcap^2,
GDPcap_l = ifelse(year == 2005, NA, dplyr::lag(GDPcap)),
GDPcap_l2 = ifelse(year == 2005, NA, dplyr::lag(GDPcap2)),
GDPcap_ll = ifelse(year == 2005, NA, dplyr::lag(GDPcap_l)),
GDPcap_ll2 = ifelse(year == 2005, NA, dplyr::lag(GDPcap_l2)),
GDPcap_lll = ifelse(year == 2005, NA, dplyr::lag(GDPcap_ll)),
GDPcap_lll2 = ifelse(year == 2005, NA, dplyr::lag(GDPcap_ll2)),
unr,
unr2 = unr^2,
unr_l = ifelse(year == 2005, NA, dplyr::lag(unr)),
unr_l2 = ifelse(year == 2005, NA, dplyr::lag(unr2)),
unr_ll = ifelse(year == 2005, NA, dplyr::lag(unr_l)),
unr_ll2 = ifelse(year == 2005, NA, dplyr::lag(unr_l2)),
unr_lll = ifelse(year == 2005, NA, dplyr::lag(unr_ll)),
unr_lll2 = ifelse(year == 2005, NA, dplyr::lag(unr_ll2)),
)
terms <- list(
c("GDPcap", "unr"),
c("GDPcap", "unr", "unr2", "GDPcap2", "unr_l", "unr_l2", "GDPcap_l",
"GDPcap_l2", "unr_ll", "unr_ll2", "GDPcap_ll", "GDPcap_ll2", "unr_lll",
"unr_lll2", "GDPcap_lll", "GDPcap_lll2"),
c("GDPcap", "GDPcap2", "GDPcap_l", "GDPcap_l2", "GDPcap_ll", "GDPcap_ll2"),
c("GDPcap_l", "GDPcap_l2", "GDPcap_ll")
)
panel.tbl <- data.frame(term = c(names(c.panel.extended)[-c(1, 2, 3)],
"Chow-teszt", "Hausman-teszt", "Korrigált R^2"))
for (i in 1:length(terms)) {
formula <- as.expression(paste("formula = tfr ~", paste(terms[[i]],
collapse = " + ")))
c.panel.pooling.extended <- plm(eval(formula),
data = c.panel.extended, model = "pooling")
c.panel.within.extended <- plm(eval(formula),
data = c.panel.extended, model = "within")
c.panel.random.extended <- plm(eval(formula),
data = c.panel.extended, model = "random")
panel.tbl <- panel.tbl %>%
merge(c.panel.within.extended %>%
broom::tidy() %>%
transmute(
term,
estimate = paste0(as.character(format(
estimate, digits = 3, nsmall = 3, decimal.mark = ",")),
case_when(
p.value < .01 ~ "***",
p.value < .05 ~ "**",
p.value < .1 ~ "*",
T ~ ""
))
) %>% rbind(
data.frame(
term = c("Chow-teszt", "Hausman-teszt", "Korrigált R^2"),
estimate = c(
pooltest(c.panel.pooling.extended, c.panel.within.extended)$p.value %>%
scales::percent(accuracy = .01, decimal.mark = ","),
phtest(c.panel.within.extended, c.panel.random.extended)$p.value %>%
scales::percent(accuracy = .01, decimal.mark = ","),
c.panel.within.extended %>% plm::r.squared(dfcor = T) %>%
scales::percent(accuracy = .01, decimal.mark = ",")
)
)
) %>% set_names(c("term", i)),
all = T
)
}
panel.tbl %>%
setNames(c("variable", as.roman(1:(ncol(.) - 1)))) %>%
mutate(variable = factor(variable, levels = c(names(c.panel.extended),
"Chow-teszt", "Hausman-teszt", "Korrigált R^2"))) %>%
arrange(variable) %>%
mutate(
variable = as.character(variable),
variable = str_replace(variable, "2", "^2"),
variable = ifelse(variable == "Korrigált R^^2", "Korrigált R^2", variable),
variable = str_replace(variable, "GDPcap", "GDP/fő"),
variable = str_replace(variable, "unr", "Munkanélküliségi ráta"),
variable = str_replace(variable, "_lll", " (l=3)"),
variable = str_replace(variable, "_ll", " (l=2)"),
variable = str_replace(variable, "_l", " (l=1)")
) %>% mutate_all(function(x) ifelse(is.na(x), "", x)) %>%
knitr::kable(
col.names = c("változó", "I.", "II.", "III.", "IV."),
align = c("l", rep("c", ncol(.) - 1)),
caption = "Becsült longitudinális modellek a TTA-ra"
)| változó | I. | II. | III. | IV. |
|---|---|---|---|---|
| GDP/fő | 6,34e-05*** | -9,61e-05 | 8,53e-05 | |
| GDP/fő^2 | 1,15e-08 | -1,33e-09 | ||
| GDP/fő (l=1) | 3,54e-04*** | 4,23e-04*** | 4,63e-04*** | |
| GDP/fő (l=1)^2 | -3,24e-08* | -3,77e-08** | -3,15e-08*** | |
| GDP/fő (l=2) | 2,00e-04* | -1,48e-04* | -8,16e-05** | |
| GDP/fő (l=2)^2 | -2,06e-08 | 9,40e-09 | ||
| GDP/fő (l=3) | -7,65e-05 | |||
| GDP/fő (l=3)^2 | 8,49e-09 | |||
| Munkanélküliségi ráta | -2,05e-02*** | -2,39e-03 | ||
| Munkanélküliségi ráta^2 | -2,66e-04 | |||
| Munkanélküliségi ráta (l=1) | 9,95e-04 | |||
| Munkanélküliségi ráta (l=1)^2 | -2,73e-04 | |||
| Munkanélküliségi ráta (l=2) | 3,21e-03 | |||
| Munkanélküliségi ráta (l=2)^2 | -2,29e-04 | |||
| Munkanélküliségi ráta (l=3) | 1,23e-02 | |||
| Munkanélküliségi ráta (l=3)^2 | -1,44e-04 | |||
| Chow-teszt | 0,00% | 0,00% | 0,00% | 0,00% |
| Hausman-teszt | 0,00% | 0,07% | 0,00% | 0,00% |
| Korrigált R^2 | 68,07% | 82,75% | 71,41% | 71,02% |
Jelölések: l=1 \(\rightarrow\) első késleltetett; \(\ast\) \(\rightarrow\) adott változó 10%-os szignifikancia szinten szignifikáns; \(\ast\ast\) \(\rightarrow\) adott változó 5%-os szignifikancia szinten szignifikáns; \(\ast\ast\ast\) \(\rightarrow\) adott változó 1%-os szignifikancia szinten szignifikáns.
A paraméterek mindegyik esetben a fixhatású-modell paramétereit mutatják. A GDP/fő ezer Forintban, míg a munkanélküliségi ráta százalékban került a modellbe.
# Hungarian map draw function
hun_map_plot <- function(df, na.value = "white", low = "white", high = "black"){
hunsf %>%
merge(set_names(df, c("NAME", "value"))) %>%
ggplot() +
geom_sf(aes(fill = value)) +
ggthemes::theme_map() +
scale_fill_viridis_c(guide = guide_colorbar(ticks.colour = 'black',
frame.colour = 'black'))
}Az első modell nem tartalmaz késleltetett magyarázó változókat, sem kvadratikus hatást megjelenítő négyzetre emelt tagokat. Ebben az esetben mind a GDP/fő, mind a munkanélküliségi ráta paramétere 1%-on szignifikáns. A második modellben szerepel a GDP/fő és munkanélküliségi ráta, ezeknek négyzetei, és mindezek késleltetett változatai, egészen a harmadik évig (miután mindössze 19 megye és Budapest idősora szerepel a modellben, így több regresszor felvételére nincs lehetőség). A második longitudinális modellben a munkanélküliségi rátának egyetlen transzformáltja sem szignifikáns, a p-értékek eseteként egy közeliek. Ennek megfelelően a harmadik modell már csak a GDP/fő transzformáltjait tartalmazza. Csak úgy, mint a második modellben az egy évvel késeltetett, az egy évvel késleltetett kvadratikus, és a két évvel késleltetett GDP/fő érték mutatkozik szignifikánsnak a modellben. Így a negyedik modell már csak ezt a három regresszort tartalmazza. A IV. modell egyedi konstansait a 8. ábra ismerteti, amelyből kivehető, hogy a TTA GDP/főtől nem függő komponense a fővárosban a legalacsonyabb, míg az észak-keleti megyékben lényegesen magasabb.
c.panel.within.extended %>%
plm::fixef() %>%
data.frame() %>%
rownames_to_column() %>%
hun_map_plot() + labs(fill = "TTA") +
theme(legend.position = "right")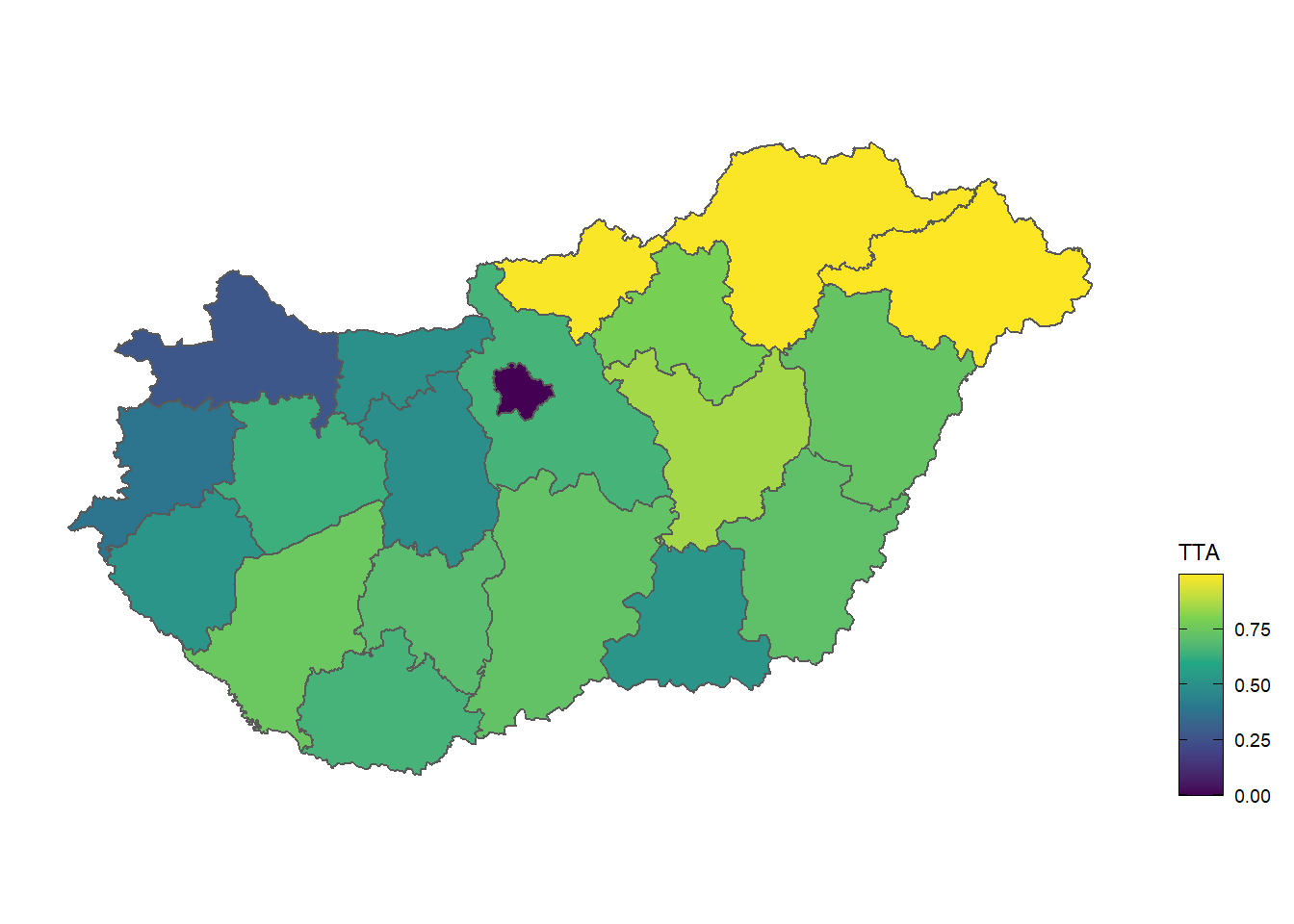
Ábra 8: A IV. longitudinális modell egyedi konstansai
Eredmények értelmezése, következtetések levonása
A II., III. és IV. longitudinális modell eredménye is arra utal, hogy a GDP/fő egy évvel késeltetett, egy évvel késleltetett kvadratikus, és a két évvel késleltetett értéke meghatározó a termékenységi ráta alakulásában. Látható, hogy a korrigált R2 igen magas, illetve a 9. ábra jeleníti meg a IV. modellel készült becsléseket, amelyeken szintén az látszik, hogy a modell igen jól írja le a TTA alakulását.
c.panel.within.extended %>%
broom::augment() %>%
dplyr::select(.rownames, .fitted) %>%
merge(c.panel %>% mutate(".rownames" = seq(nrow(c.panel)))) %>%
transmute(Becsült = .fitted, Valós = tfr, county = str_remove_all(county,
paste(c(" megye", "-Csanád"), collapse = "|")), year = year) %>%
pivot_longer(1:2) %>%
ggplot(aes(x = as.numeric(year), y = value, color = name)) +
geom_line(size = 1.2) +
scale_x_continuous(expand = c(0, 0), breaks = seq(2008, 2016, 4)) +
scale_color_grey() +
facet_wrap(~county, ncol = 4) +
labs(x = "Év", y = "TTA", color = NULL)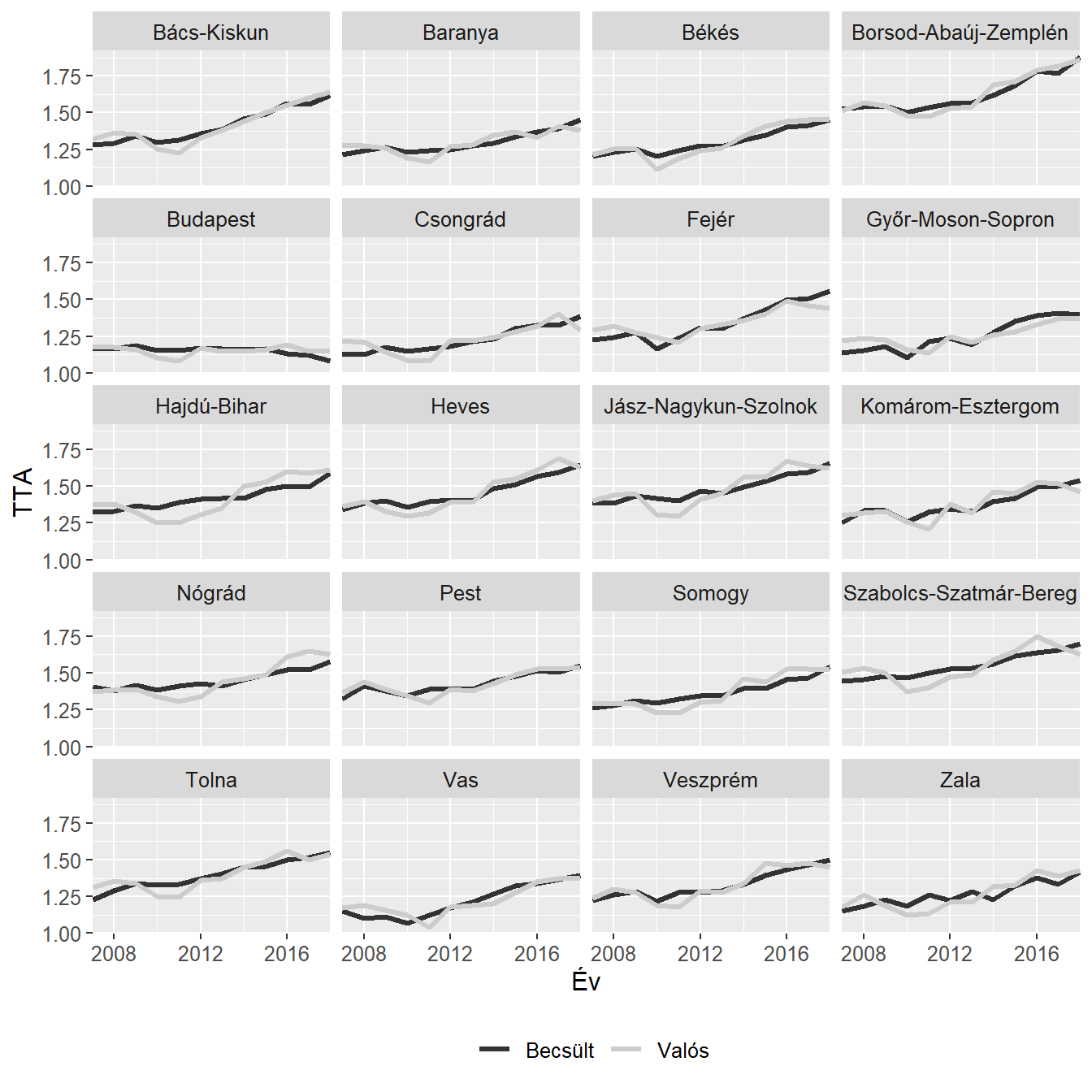
Ábra 9: TTA becslése megyénként a fix modellel
A szignifikánsnak bizonyult regresszorok köre a fentebb közölt VAR modellek eredményei alapján a vártnak megfelelőek. Ami újonnan kinyert és releváns információ, hogy GDP/fő négyzetének késleltetett értéke is szignifikáns, illetve előjele negatív, tehát a GDP/fő növekedésének hatása a TTA-ra nézve ellaposodó. Ezt a hatást jeleníti meg a 10. ábra. Jól kivehető, hogy a termékenységi rátára való hatása az egy főre eső GDP-nek 7340 ezer Forint után már nem növelő, hanem csökkentő. Az egyetlen területi egység, melynek GDP/fő értéke ezt meghaladja az Budapest. Mindez azt jelenti, hogy a termékenységi ráta emelésében szükséges a szegényebb területek (Nógrád megye, Szabolcs-Szatmár-Bereg megye, Békés megye) bruttó kibocsátásának emelése, mert ott egységnyi GDP/fő emelkedés nagyobb hatást ér el. Ez az eredmény egyenesen szembe megy annak, amit internacionális elemzések korábban a GDP/fő és a TTA közti kapcsolatról leírtak (Kreiszné Hudák 2019:207).
Miután a 2. késleltetés is szignifikáns, negatív előjellel, így arra a következtetésre jutunk, hogy minden változatlanság mellett a GDP/fő növekedését követően a második évben némileg alacsonyabb lesz a TTA, mint az első évben, de ez a hatás nagyságrendekkel kisebb.
ggplot(data.frame(x = c(0, 10000)), aes(x = x)) +
stat_function(fun = function(x)
x*c.panel.within.extended$coefficients["GDPcap_l"] +
x^2 * c.panel.within.extended$coefficients["GDPcap_l2"], size = 2) +
geom_vline(xintercept = c.panel %>%
filter(year == 2018) %>%
pull(GDPcap) %>%
.[-1], linetype = "dashed") +
geom_vline(aes(linetype = "Magyar megyék egy főre eső GDP értékei",
xintercept = (c.panel %>% filter(year == 2018) %>%
pull(GDPcap) %>% .[1]))) +
scale_linetype_manual(values = "dashed") +
scale_x_continuous(expand = c(0, 0)) +
scale_y_continuous(expand = c(0, 0), limits = c(0, 2)) +
labs(x = "GDP/fő (ezer Ft-ban) (l = 1)",
y = "Egyedi konstanson felüli TTA érték", linetype = NULL) +
theme(plot.margin = unit(c(1, 1, 1, 1), "cm"))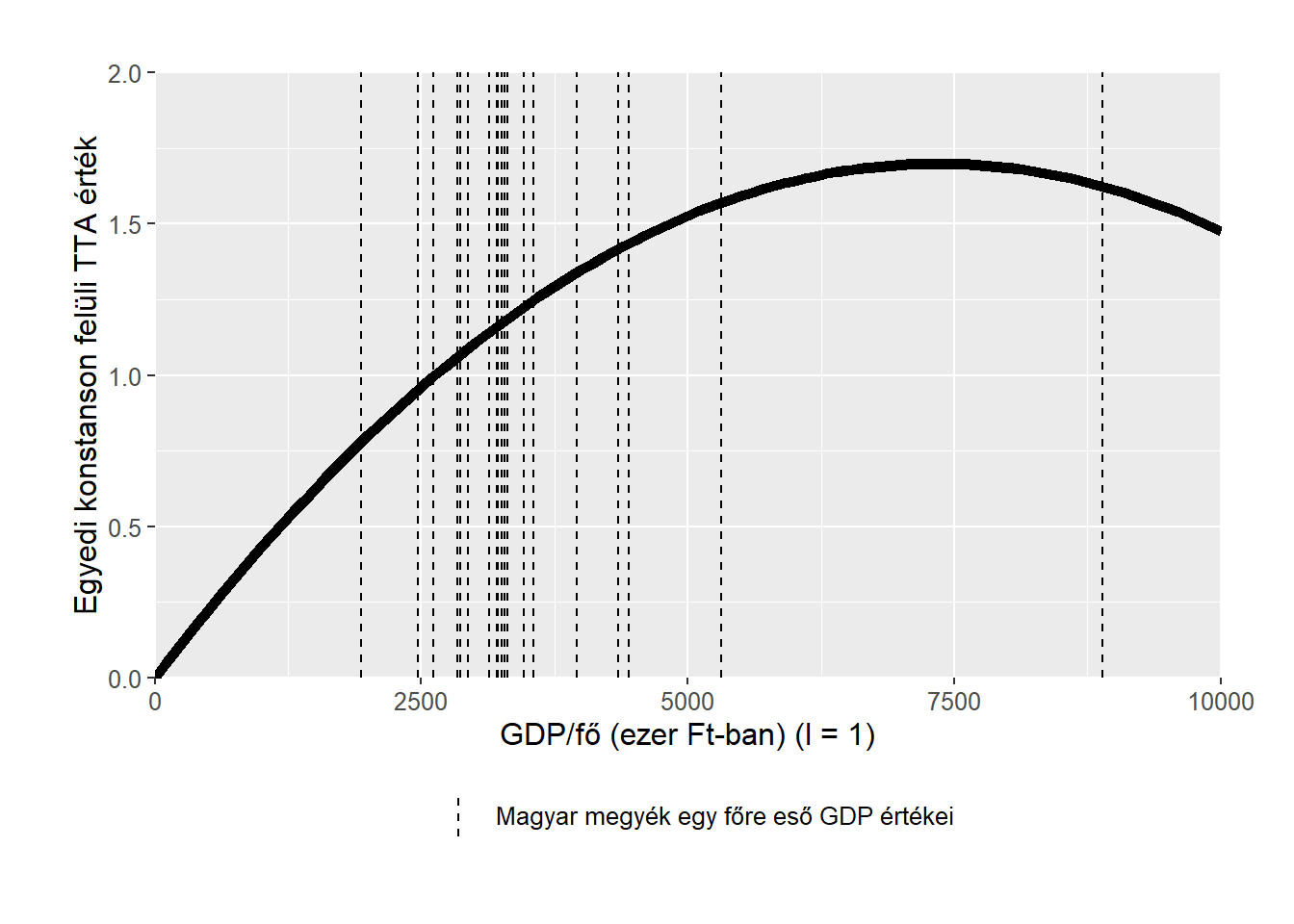
Ábra 10: A GDP/fő hatása a TTA-ra a IV. panel modell alapján