6 Introduction to simulation
6.1 Motivation
Creating simulated data set is a common habit to test your methodology and get familiar with it. Papers based on simulated data are usually the most profitable ones.However, writing code for simulation is much more effective if you do not use million of loops, because the script can easily become messy and hard to read.
That is the reason, while we learn some theoretical concepts about how to effectively write simulations.
6.2 The for loop
Sadly, a common way to write iteration with loops.
for (i in 1:5) {
print(i)
}
#> [1] 1
#> [1] 2
#> [1] 3
#> [1] 4
#> [1] 5This is a simple syntax for printing the numbers from 1 to 5. for loop works as a snippet, so you have to only type “for” and press TAB after. This will create the frame work (spaces, inputs, parentheses) of the loop. You should see then the following:
for (variable in vector) {
}
#> Error in for (variable in vector) {: invalid for() loop sequenceNow you have to specify the input: the variable, the vector and the code to evaluate.
6.3 Replicate
replicate is a base R function, but can be very useful. An important difference is that with loop, you can refer to an iterator (i = which iteration runs?). But that is something you do not need in simulative studies, so i would be only a redundant variable in your environment. Lets generate a random set from normal distribution.
rnorm(n = 10, mean = 0, sd = 1)
#> [1] 1.53071072 1.11572128 -1.75680548 0.72440956 -0.42208816 -0.81778805
#> [7] 0.24025204 -0.03659535 1.64694641 0.59957410Lets generate 5 sets with replicate.
replicate(n = 5, rnorm(n = 10, mean = 0, sd = 1))
#> [,1] [,2] [,3] [,4] [,5]
#> [1,] -1.0724047 0.1045381 -0.6821441 0.50552179 -2.1724049
#> [2,] -0.5170869 -1.3029887 -0.3407339 -0.26928148 0.7668037
#> [3,] 0.5090504 -0.2540999 0.2150593 -0.68754642 -0.2515032
#> [4,] 0.8061063 2.6600309 -0.5483644 -1.44132060 0.1812080
#> [5,] -0.1964774 1.6424674 1.2690177 0.57432540 -0.8727565
#> [6,] 1.0609074 -0.3389844 0.8434366 0.16891814 0.5702774
#> [7,] 0.4528373 0.2114825 -0.5460979 -0.51564255 -0.5184491
#> [8,] 0.1612659 -0.8790304 0.3836906 0.75262964 0.4892118
#> [9,] -0.3785246 -1.1249163 1.5422579 -0.42230031 -1.2927494
#> [10,] -1.2660102 -0.1263657 -1.0911051 -0.02975666 1.6548887The result is a matrix, but if you wish to keep the output in list format you can write the following:
replicate(n = 5, rnorm(n = 10, mean = 0, sd = 1), simplify = FALSE)
#> [[1]]
#> [1] 1.2736958 -0.6688812 -1.3302128 0.5530845 -0.1607211 0.1988171
#> [7] 0.1283606 0.3499840 0.7122512 0.8923841
#>
#> [[2]]
#> [1] -0.47361369 0.74955592 -0.39576259 -0.94361428 -0.46896246 0.02996324
#> [7] 0.21263376 0.66298590 0.24973523 -0.59405192
#>
#> [[3]]
#> [1] 3.22318891 0.86463075 -0.45963259 1.60003864 -1.17521562 1.30286863
#> [7] 0.12279515 -0.22744636 1.00398994 -0.07896539
#>
#> [[4]]
#> [1] -2.39293563 -0.45604575 0.15624406 -0.72389236 0.49026891 1.57235957
#> [7] -2.39689102 0.91221690 -0.01008771 -1.01214036
#>
#> [[5]]
#> [1] -2.8694232 2.5789621 0.5585526 1.0734009 -0.3474956 0.8562965
#> [7] 0.5296800 0.0107040 0.5775843 0.9275607But how to use the simulated data, what we have created? Lets recall, that we can use a function on each elements of a list or vector with the map function. (map_dbl if the output contains only one number per element)
replicate(n = 5, rnorm(n = 10, mean = 0, sd = 1), simplify = FALSE) %>%
map(mean) # mean of trajectories as a list
#> [[1]]
#> [1] 0.4386977
#>
#> [[2]]
#> [1] -0.4110464
#>
#> [[3]]
#> [1] -0.2545167
#>
#> [[4]]
#> [1] -0.1256227
#>
#> [[5]]
#> [1] 0.4292195
replicate(n = 5, rnorm(n = 10, mean = 0, sd = 1), simplify = FALSE) %>%
map_dbl(mean) # mean of trajectories as a vector
#> [1] -0.77554025 -0.12528062 0.05073575 -0.09084027 0.15321429The advantage of ignoring loops from your script for simulation is the increase in speed. In this aspect, it is important to note that you can use parallel computing to make your code even faster5.
6.4 The tidy framework
From the previous chapters we already know that we nest even data frames (and any other object) into a data frame.
Lets create a data frame first with the corresponding parameters.
simulation_df <- tibble(
m = 100, # mean
s = 20, # sd
)
simulation_df
#> # A tibble: 1 x 2
#> m s
#> <dbl> <dbl>
#> 1 100 20Lets add a set of random data from normal distribution, with the given mean.
simulation_df %>%
mutate(
data = map(m, ~ rnorm(n = 10, mean = .)) # . refers to the m which is mean
)
#> # A tibble: 1 x 3
#> m s data
#> <dbl> <dbl> <list>
#> 1 100 20 <dbl [10]>We see that a numeric vector (double) is nested into a cell of the data frame. Are we interested in the minimum of the simulated data? Lets use map again.
simulation_df %>%
mutate(
data = map(m, ~ rnorm(n = 10, mean = .)),
minimum = map(data, min) # minimum of the value on `data` column
)
#> # A tibble: 1 x 4
#> m s data minimum
#> <dbl> <dbl> <list> <list>
#> 1 100 20 <dbl [10]> <dbl [1]>But the new column still contains a vector, we do not see the value even if it is just a number. Remember, if we know that the result is single number, then we can convert it to numeric vector with map_dbl.
simulation_df %>%
mutate(
data = map(m, ~ rnorm(n = 10, mean = .)),
minimum = map_dbl(data, min) # minimum of the value on `data` column
)
#> # A tibble: 1 x 4
#> m s data minimum
#> <dbl> <dbl> <list> <dbl>
#> 1 100 20 <dbl [10]> 97.4Now the expected mean of the generated data is 100, but the standard deviation is still 1 (the default value). We can control for 2 input with map2.
simulation_df %>%
mutate(
data = map2(m, s, ~ rnorm(n = 10, mean = .x, sd = .y)), # .x refers to m, .y to s
minimum = map_dbl(data, min)
)
#> # A tibble: 1 x 4
#> m s data minimum
#> <dbl> <dbl> <list> <dbl>
#> 1 100 20 <dbl [10]> 61.2What about the size of the sample? We need a new frame and a new function: pmap. Use this map type function (same functionality) when you have more than 2 inputs.
simulation_df <- tibble(
m = 100, # mean
s = 20, # sd
n = 1000, # sample size
)
simulation_df
#> # A tibble: 1 x 3
#> m s n
#> <dbl> <dbl> <dbl>
#> 1 100 20 1000
simulation_df %>%
mutate(
data = pmap(list(m, s, n), function(m, s, n) rnorm(n = n, mean = m, sd = s))
)
#> # A tibble: 1 x 4
#> m s n data
#> <dbl> <dbl> <dbl> <list>
#> 1 100 20 1000 <dbl [1,000]>But why do we worked so much to generate a simply trajectory? We could do this simply with the rnorm function. It is true, but most of the time you have to generate multiple random data sets with different arguments. Lets see how to manage this with the current frame work.
simulation_df <- tibble(
m = c(1, 10, 100), # mean
s = c(3, 10, 50), # sd
n = c(10, 100, 10000) # sample size
)
simulation_df
#> # A tibble: 3 x 3
#> m s n
#> <dbl> <dbl> <dbl>
#> 1 1 3 10
#> 2 10 10 100
#> 3 100 50 10000
simulation_df %>%
mutate(
data = pmap(list(m, s, n), function(m, s, n) rnorm(n = n, mean = m, sd = s)),
minimum = map_dbl(data, min),
maximum = map_dbl(data, max)
)
#> # A tibble: 3 x 6
#> m s n data minimum maximum
#> <dbl> <dbl> <dbl> <list> <dbl> <dbl>
#> 1 1 3 10 <dbl [10]> -2.41 8.37
#> 2 10 10 100 <dbl [100]> -15.9 28.5
#> 3 100 50 10000 <dbl [10,000]> -103. 278.So we see that the variables definied in the mutate function will be calculated for every input combination in the frame. How about to evaluate it multiple times? We have to duplicate the lines.
slice can be used to select a given row with number.
simulation_df %>%
slice(2) # select the 2nd line
#> # A tibble: 1 x 3
#> m s n
#> <dbl> <dbl> <dbl>
#> 1 10 10 100But what if the number appears multiple times?
simulation_df %>%
slice(c(2, 2)) # select the 2nd line 2 times
#> # A tibble: 2 x 3
#> m s n
#> <dbl> <dbl> <dbl>
#> 1 10 10 100
#> 2 10 10 100So we need to select each line multiple times. We can do it with the rep function.
rep(c(1, 2, 3), times = 3)
#> [1] 1 2 3 1 2 3 1 2 3
rep(c(1, 2, 3), each = 3)
#> [1] 1 1 1 2 2 2 3 3 3
simulation_df %>%
slice(rep(1:n(), each = 2)) # select all the lines 2 times
#> # A tibble: 6 x 3
#> m s n
#> <dbl> <dbl> <dbl>
#> 1 1 3 10
#> 2 1 3 10
#> 3 10 10 100
#> 4 10 10 100
#> 5 100 50 10000
#> 6 100 50 10000
simulation_df %>%
slice(rep(1:n(), each = 2)) %>% # select all the lines 2 times
mutate(
data = pmap(list(m, s, n), function(m, s, n) rnorm(n = n, mean = m, sd = s)),
minimum = map_dbl(data, min),
maximum = map_dbl(data, max)
)
#> # A tibble: 6 x 6
#> m s n data minimum maximum
#> <dbl> <dbl> <dbl> <list> <dbl> <dbl>
#> 1 1 3 10 <dbl [10]> -4.69 4.59
#> 2 1 3 10 <dbl [10]> -4.56 5.78
#> 3 10 10 100 <dbl [100]> -12.6 31.6
#> 4 10 10 100 <dbl [100]> -16.3 29.8
#> 5 100 50 10000 <dbl [10,000]> -110. 304.
#> 6 100 50 10000 <dbl [10,000]> -75.0 274.6.5 Case Study
How does the kurtosis change if the sample size or the standard deviation changes?
tibble(n = 10^(0:5)) %>%
crossing(s = 2^(0:5)) # match all possible combination
#> # A tibble: 36 x 2
#> n s
#> <dbl> <dbl>
#> 1 1 1
#> 2 1 2
#> 3 1 4
#> 4 1 8
#> 5 1 16
#> 6 1 32
#> 7 10 1
#> 8 10 2
#> 9 10 4
#> 10 10 8
#> # ... with 26 more rows
tibble(n = 10^(1:5)) %>%
crossing(s = 2^(0:5)) %>% # match all possible combination
mutate(
data = map2(n, s, ~ rnorm(n = .x, sd = .y)) # generate the data
)
#> # A tibble: 30 x 3
#> n s data
#> <dbl> <dbl> <list>
#> 1 10 1 <dbl [10]>
#> 2 10 2 <dbl [10]>
#> 3 10 4 <dbl [10]>
#> 4 10 8 <dbl [10]>
#> 5 10 16 <dbl [10]>
#> 6 10 32 <dbl [10]>
#> 7 100 1 <dbl [100]>
#> 8 100 2 <dbl [100]>
#> 9 100 4 <dbl [100]>
#> 10 100 8 <dbl [100]>
#> # ... with 20 more rows
tibble(n = 10^(1:5)) %>%
crossing(s = 2^(0:5)) %>% # match all possible combination
mutate(
data = map2(n, s, ~ rnorm(n = .x, sd = .y)),
kurt = map_dbl(data, moments::kurtosis) # calculate the kurtosis of the data
)
#> # A tibble: 30 x 4
#> n s data kurt
#> <dbl> <dbl> <list> <dbl>
#> 1 10 1 <dbl [10]> 1.61
#> 2 10 2 <dbl [10]> 3.43
#> 3 10 4 <dbl [10]> 2.01
#> 4 10 8 <dbl [10]> 1.75
#> 5 10 16 <dbl [10]> 2.56
#> 6 10 32 <dbl [10]> 2.27
#> 7 100 1 <dbl [100]> 2.67
#> 8 100 2 <dbl [100]> 3.02
#> 9 100 4 <dbl [100]> 2.60
#> 10 100 8 <dbl [100]> 2.65
#> # ... with 20 more rows
tibble(n = 10^(1:5)) %>%
crossing(s = 2^(0:5)) %>%
slice(rep(1:n(), each = 100)) %>% # increase the iterations to 100
mutate(
data = map2(n, s, ~ rnorm(n = .x, sd = .y)),
kurt = map_dbl(data, moments::kurtosis)
) %>%
ggplot() + # plot
aes(kurt) +
geom_density() +
facet_grid(n ~ s)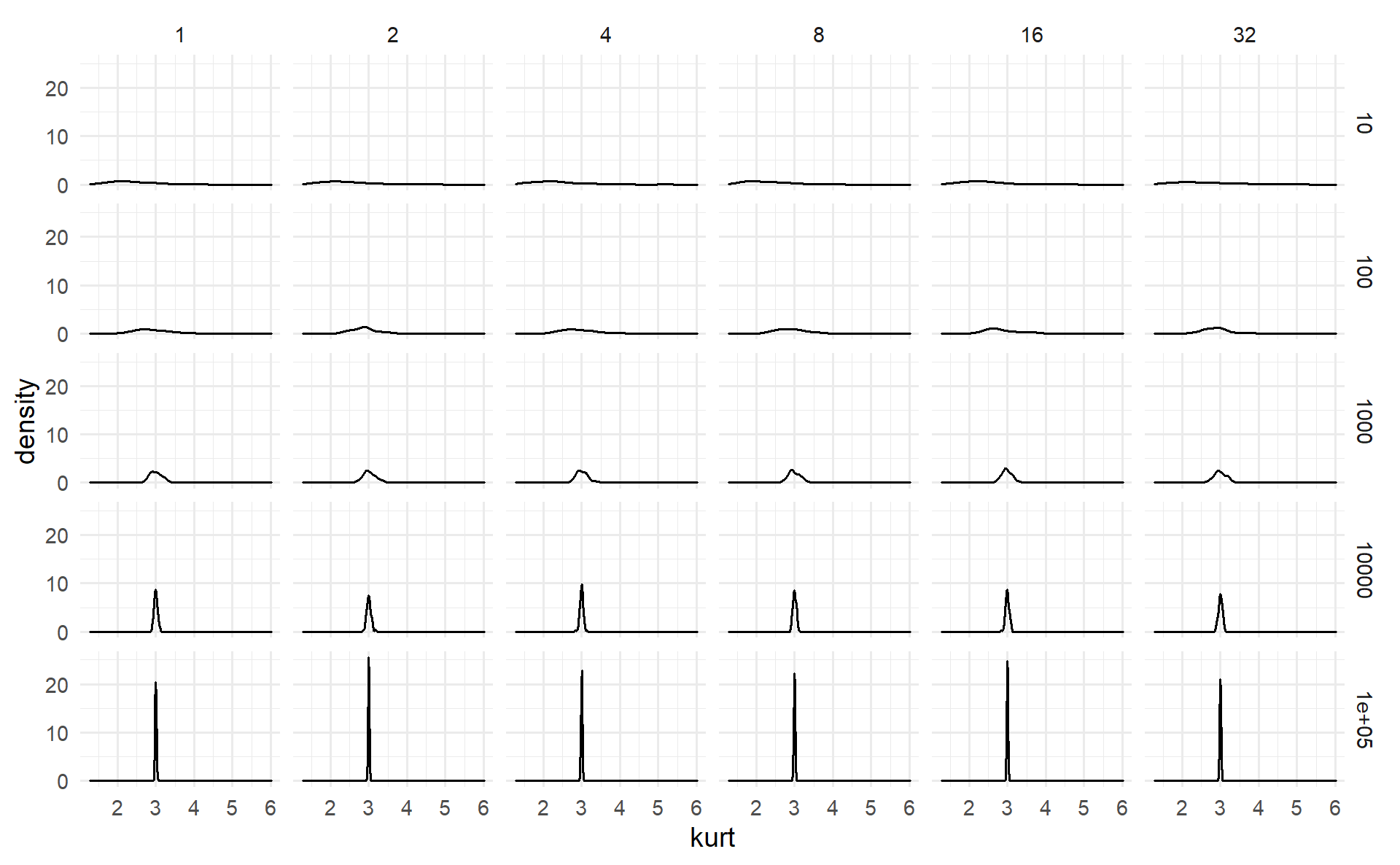
Conclusion #1: The kurtosis of the sample size did not change if we increase the standard deviation or the sample size. But is has became concentreted to 3, when the size of the sample increased.
Conclusion #2: We could write a complex simulation with 7 simple codes (while 4 lines are related to the plot).